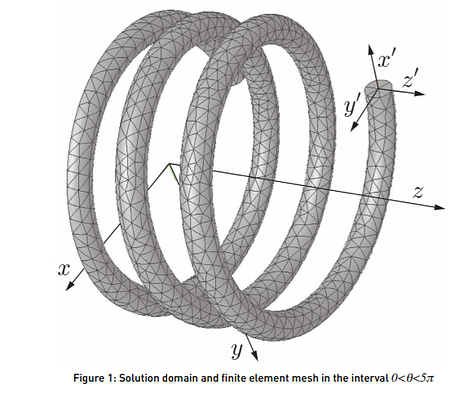
The finite element mesh used in the reference solution for the NAFEMS FEA Puzzler (courtesy NAFEMS).

In a February 2019 S.A.F.E.R. Simulation post, ESRD provided a teaser video of the October 2018 NAFEMS FEA Puzzler solution, in which the incremental spring rates for a 3D coil spring were numerically investigated. In NAFEMS’ July 2019 edition of Benchmark Magazine, ESRD Chairman Dr. Barna Szabó reveals the converged Numerical Simulation solution for the incremental spring rates, provides a summary of the FEA Puzzler respondent submissions, and documents the various approaches taken by the respondents.

As a refresher, the original October 2018 NAFEMS FEA Puzzler description was as follows:

FEA Puzzler from NAFEMS Benchmark Magazine October 2018

Reference Solution

Below is a short summary of Dr. Szabó’s reference solution results, computed with ESRD’s StressCheck and verified by numerical convergence studies (all images courtesy NAFEMS):

The finite element mesh chosen for the reference solution is shown in Figure 1. The mesh is comprised of 9,691 tetrahedral isoparametric (10-node) elements, and solved by p-extension from p=2 to 5.

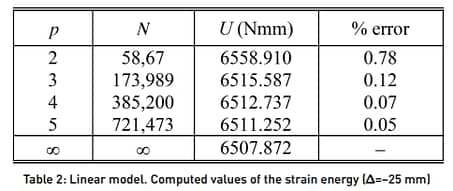
Table 2 summarizes the computed values of strain energy, U, associated with each polynomial level, p, and degrees of freedom, N:

The spring rate, k, may be computed from the strain energy, U, and imposed spring displacement, Δ, using the following equation:

k = 2*U/Δ²

Using the extrapolated value of U, in which N→∞, we compute k = 20.83 N/mm for an imposed spring displacement Δ=-25 mm.

From the NAFEMS FEA Puzzler solution article:

The estimated relative error in k is less than 0.05%. Note that this error does not account for the curved surfaces being approximated by piecewise quadratic polynomials. However, given the large number of 10-node tetrahedra (see Figure 1), the errors of approximation in the surface representation can be neglected.

More generally, the stiffness of the spring can be computed by energy methods. These methods are superconvergent.

Download the Full NAFEMS Article

The entire NAFEMS FEA Puzzler article, complete with the computation of the spring rate via linear and geometric nonlinear force resultants (also shown to be k=20.8 N/mm), comparison with classical methods (k=19.33 N/mm), a summary of respondent submissions, and additional commentary, may be downloaded at the following link:

Note: There is a typo in Equation 1 on page 28 of the NAFEMS article. The value of k in Equation 1 should be 20.83 N/mm and not 25.83 N/mm.