Introduction

A multi-body contact capability has been implemented in StressCheck to account for frictionless mechanical contact in the context of the p-version of the finite element method. A few notes about StressCheck’s close-contact implementation:

• The implementation is available for Planar, Extrusion, Axisymmetric and 3D elasticity problems under the assumptions of small-strain/small-deformation.
• Material nonlinearities of the contacting bodies can also be incorporated in the analysis.
• The effect of geometric nonlinearities are not yet available.
• With the release of StressCheck v12.0, the implementation supports the automatic detection and assignment of contact between boundaries that lie within a proximity tolerance.

For a brief demonstration of StressCheck’s implementation of multi-body contact for a knuckle joint, refer to StressCheck Demo: 3D Multi-Body Contact Analysis.

Formulation

The approach, using a contact element formulation that does not require mesh conformity between contacting surfaces, is based on the principle of minimum potential energy subjected to the proper kinematic conditions at the contacting surfaces.

The problem must be solved by an iterative procedure to determine the contact regions and has been treated using the augmented Lagrangian method; for details we refer to “Solution of Contact Problem using the hp-Version of the Finite Element Method” by I. Páczelt, B. A. Szabó and T. Szabó, Computers and Mathematics with Applications, Vol. 38, 49-69, 1999. The method is briefly described in the following.

Contact Gap/Pressure Relations

Consider two elastic bodies: body 1 (yellow) and body 2 (blue), with a declared contact region as indicated schematically below. A normal spring of constant K_c is placed along the contact surfaces of each body:

Let u_n1 be the normal displacement (positive if outward) at any point along the declared contact region of body 1, and u_n2 the corresponding normal displacement of body 2. The first step in the contact analysis is to determine the initial gap between the contacting surfaces. This is accomplished by projecting normal vectors from each control point of one contact zone to the element faces belonging to the opposite contact zone. The distance between the point and its projection determines the initial gap (g₀). Therefore the gap function (g) is given by:

If g < 0, then body 1 is penetrating the body 2. The condition to be satisfied for each contact region is:

where P is the pressure in the contact zone and g is the corresponding gap. During each iteration of the contact solution procedure, the values of u_n1 and u_n2 are recomputed and the value of the gap updated. For the ith iteration, the contact pressure (P) is computed as:

The corresponding normal tractions in the contact region of the body 1 (yellow) are then given as:

The traction applied at each point outside the penetration region (corrective traction when g > 0) is needed to cancel the effect of the contact spring. Similarly, the tractions for body 2 (blue) are:

After each iteration, the maximum pressure between the contacting surfaces is measured to determine whether a significant change has occurred since the previous iteration.

• If the change is larger than a pre-specified tolerance, then the iterative procedure continues.
• If the change in pressure is less than the tolerance, then the analysis procedure is terminated, and the solution vectors are available for postprocessing.

Stiffness Matrix Computation

With this implementation, the stiffness matrix for each body is computed only once and the effect of the contact is incorporated in the load vector by updating the tractions in the contact zone according to the equations T_n1 and T_n2.

The solution is very efficient because only the right hand side of the system of equations is updated in each iteration. However this solution strategy does not account for material or geometric nonlinearities.

• Material nonlinearities can be incorporated after the initial contact solution was obtained.
• Geometric nonlinearities are not considered in this implementation.

For more details about StressCheck’s multi-body contact implementation and formulation, refer to Numerical Simulation Series: Mechanical Contact.

Defining a Multi-Body Contact Analysis

With the release of StressCheck v12.0, the user now has the option to either manually define/assign the regions in contact, or ask StressCheck to automatically perform this function based on surface proximity (via a combination of the Assembly Meshing option and the Auto Contact constraint method).

Manual Contact Setup

To manually define a multi-body contact analysis with the bodies having linear or nonlinear material properties, proceed as follows:

• Create (or import) the geometric description of the bodies, (optionally) imprint bodies/create parts, and create the mesh for each body to be solved in multi-body contact.
  • There is no need to have mesh conformity between contacting surfaces.
  • However, surface conformity is recommended to ensure neighboring contact zones are equivalent.
• Create Contact Zones (Mesh tab, Create > Contact Zone) by selecting surfaces or faces in 3D and curves or edges in 2D.
  • At least two contact zones must be created for each potential contact pair.
• Define and assign material properties to all the elements as done for a standard linear or material nonlinear analysis.
• Apply the mechanical/thermal loads to the bodies as done for any analysis.
• Specify the constraints for each body and activate the contact zones by connecting the contact zone pairs. Active manually-generated contact pairs will be displayed with a light blue color.
  • Ensure there are sufficient rigid body constraints for each body in multi-body contact.
  • A contact constant (Kc) must be provided – either manually entered by the user, or automatically generated by the program if the ‘Generate’ button is pressed (see Note about the contact constant below).
  • In general, the contact constant should be selected based on the moduli of elasticity of the materials in contact, in such a way that its value is between 0.1 and 1.0 times the value of the smallest modulus of elasticity (0.1Emin < Kc < Emin) when using US units (psi), and between 0.004 and 0.04 times the value of the smallest modulus of elasticity (0.004Emin < Kc < 0.04Emin) when using SI units (MPa). The units for the contact constant are [F/L/L2].
• Convert the element mapping in active contact zones to geometric (Tools > Convert Element Mapping > Geometric (Active Contact Zones Only).
  • This ensures the gap function is measured at the highest quality resolution (see Note about element mapping below).

The below animation demonstrates the creation of a pair of contact zones for future contact constraint assignment:

For an example of modeling a 3D skin-stiffener-fastener assembly in multi-body contact, refer to StressCheck Tutorial: 3D Modeling of a Skin-Stiffener-Fasteners Assembly (Full Contact).

Automatic Contact Setup

To automatically define a multi-body contact analysis with the bodies having linear or nonlinear material properties, first enable the Assembly Meshing toggle under Mesh tab > Create > Mesh > Auto before automeshing the selected bodies. Once the Assembly Meshing toggle is enabled, then the following sequence will be performed once the Automesh button is clicked:

• Surfaces within a proximity tolerance (Default=1e-5 units if US customary, 1e-2 units if SI) will be flagged for contact candidacy.
• The automesher will then attempt to match the element faces across surfaces within the proximity tolerance.
  • Note: there is no need to split surfaces via imprint (or other solid modeling operations) beforehand, as this will be done internally as part of the assembly automeshing algorithm.
• Contact zones will automatically be generated on all matched element faces.
  • Note: updating the assembly automesh will automatically update the element faces defining the contact zones.
• Contact constraints will be automatically generated between neighboring contact zone pairs via the Auto Contact method. This method incorporates the following assumptions on the computation of the contact constant for each contact constraint:
  • If material properties are not initially assigned to the associated elements, then the contact constraints will have an empty contact constant.
  • Once material properties are assigned to the associated elements, either before or after assembly meshing is invoked, then the contact constraints will include the automatic computation of a contact constant according to recommended best practices.
  • Note: updating material property coefficients will automatically update the associated contact constants, unless the contact constant has been replaced by a parameter. Once replaced by a parameter, these contact constraints will be displayed in a green color.
• By default, the Auto Contact method generates all contact constraints as the “Contact” option, which will use the traditional multi-body contact algorithm.
  • Other options include “Fused”, which will fuse/bond fully matched element faces such that the element faces share displacements, and “Free”, which will assume there is no displacement interaction or contact pressure computed between element faces (free faces).
  • The user modify any auto-generated contact constraint to use any of the three (3) options.
  • Auto-generated “Contact” constraints will be displayed in a teal blue color, auto-generated “Fused” constraints will be displayed in a dark grey color, and auto-generated “Free” constraints will be displayed in a light grey color.
  • Note: the “Fused” option requires all node locations between matched faces to be coincident. The “Contact” and “Free” options do not have this requirement.
• Setting the A/O/M to Select > Contact Zone > Auto Contact and clicking on an active contact zone will result in the retrieval of the associated contact constraint record.

The below animation demonstrates the automatic generation of contact pairs via the Assembly Meshing feature:

A Note About Manually Generated Contact Zones

It is important to follow some guidelines when manually creating contact zone pairs to improve the efficiency of the solution. These include:

• Create contact zone pairs of similar sizes on each body. Avoid creating contact pairs in which one contact zone is much larger (or smaller) than the other. There is no intrinsic problem with this, except for the efficiency of the solution.
• When creating a contact zone for one of the contact pairs try to avoid multi intersection of the normal. To recognize the multi intersection simple consider a point on one of the contact zones and imagine a normal to the surface of the body at that point. If the normal intersects the other contact zone in more than one place, then you have a multi intersection situation. Again, there is no intrinsic problem with this, except for the efficiency of the solution.
• Avoid contact zones that span over too many elements. Whenever possible split large contact regions in smaller groups if overlapping of the contact pairs can be avoided.

The below animation demonstrates how Body-Imprint is used to optimize surfaces for contact zone creation:

For more information on optimizing geometry for 3D multi-body contact, refer to Helpful Hints and Tips: Optimization of a Simple 3D Contact Problem. Note: performing Body-Imprint operations is not required if the Assembly Meshing option is enabled, as the program will automatically perform body-imprints internally before automatically generating the contact zones.

A Note About Selecting the Contact Constant

The contact constant (K_c) is used during the iterative contact solution procedure to evaluate the contact pressure between each iteration. When specifying contact constraints to connect contact zone pairs, the user must define K_c either by entering a value manually or by pressing the ‘Generate’ button which allows the program to automatically compute the contact constant according to the following:

For US units (lbf/in3):

• K_c = 0.1 * min(Eⁱ) if isotropic or
• K_c = 0.1 * min(E₁₁ⁱ,E^j) if orthotropic/laminate

For SI units (N/mm3) use:

• K_c = 0.004 * min(Eⁱ) if isotropic or
• K_c = 0.004 * min(E₁₁ⁱ,E^j) if orthotropic/laminate

where min(Eⁱ) or min(E₁₁ⁱ,E^j) is the minimum value of the elastic modulus (on the first direction for orthotropic or laminated materials) for all elements i, j associated to a given contact pair.

For automatic generation of the contact constant, if no elements are associated with at least one of the selected contact zones, or no material properties have been assigned for at least one of the elements associated with the contact zones, the contact constant is not generated and an error is issued indicating the missing conditions.

Remark: The automatic generation of the contact constant does not produce an associative relationship with the material properties. If the material properties referenced by the contact zones are changed, the generated value of an existing record will not be updated.

The below animation demonstrates how the recommended contact constant may be automatically generated during contact pairing:

For more information about selecting the optimal contact constant for a particular multi-body contact application, refer to How Do I Select Contact Constant For Multi-Body Contact?

A Note About Sufficient Constraints

Each body of a multi-body contact problem must have enough constraints for obtaining the solution. The presence of the contact zone is equivalent to having a normal spring acting on the declared contact region. If no other constraints are present in the body, it is important to ascertain whether the body can have rigid body displacement or rotations. If it does, it is necessary to add nodal constraints records to prevent the rigid body modes.

Alternatively, if the model is such that the rigid body constraints may take reactions, light normal/tangent springs (<<< min(E)) are recommended to prevent the rigid body nodes.

For more information on constraining rigid body motion, refer to Helpful Hints and Tips: Constraining Rigid Body Motion.

A Note About Element Mapping

When the MeshSim automatic mesh generator is used to create the mesh of a multi-body contact problem, at solution time the program automatically converts the quadratically mapped elements associated with the active contact zones to geometric elements.
If one or more elements fail to convert, they are retained as quadratically mapped, while those that converted correctly are retained as geometric. This can create a local perturbation in the contact region that may affect the quality of the solution (after the solution is complete, check the error log to see if any elements failed the mapping conversion).

The recommended action is to change the meshing parameters so that the mapping conversion is successful for all the elements in the contact regions. To convert the mapping and check whether the conversion is successful before running the analysis, simply select the option Convert Element Mapping in the Tools menu and then select Geometric (Active Contact Zones Only). An error report will be issued if some elements fail to convert to geometric mapping. Local mesh refinement may be required to correct the mapping issue.

For more information about the influence of mixed mapping on results, refer to Can I Solve Models with Mixed Element Mapping?

Executing a Multi-Body Contact Analysis

After defining the solution ID record, perform a linear analysis.

• The program will recognize the presence of the contact constraints and perform the necessary iterations until the variation in the maximum contact pressure is less than 0.01% (or a user-specified Pressure Tolerance) or the number of iteration reaches 40 (or a user-specified Iteration Limit).
  • During the gap measurement, if a Ray Tolerance has been specified (in length units) StressCheck will limit the search of the contact neighbor to within the specified distance. For example, in the case of a pin inside a hole, there are two possible neighbors on the pin for each point on the hole. Defining a Ray Tolerance value to be smaller than the diameter of the pin will limit the search only to the closest point.
  • The Iteration Limit must be an integer >=10 and <=100.
  • The Pressure Tolerance must be a positive value <=10%.
  • For more information about the Contact Settings and when they should be changed, consult What Are Some Common Multi-Body Contact Issues? and StressCheck Tutorial: Multi-Body Contact Solver Options/Plot Functions.
• When solving a contact analysis problem, the associated live error update in the solver window is now more appropriately labeled as the “Max Contact Pressure Error.”
  • Additionally, the element number associated with the reported error value is also displayed in the solver window. This allows the user to quickly pinpoint which region has the highest contact pressure error. This information is also recorded in the Project Log for future reference.

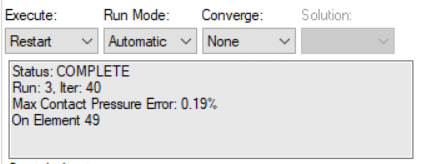
For an example of setting up and executing a 3D fitting/I-beam multi-body contact analysis, refer to StressCheck Tutorial: Fitting + I-Beam Multi-Body Contact Analysis.

A Note on Multi-Body Contact Efficiency

In some cases, it is possible to improve the solve time for multi-body contact analyses. This may be accomplished through combinations of hand-meshing and automeshing, p-Discretization and/or localized mesh refinement:

For more details on improving multi-body contact efficiency, refer to How Can I Improve Multi-Body Contact Efficiency?

A Note About Plasticity and Contact

To account for material nonlinearities, a dual iteration process is used.

• During the first iterative procedure, the tractions in the contact regions are determined assuming that the material remains linear.
• Once convergence was achieved, the second iterative procedure is initiated by modifying the stiffness matrices of those elements which are affected by plasticity, while the tractions in the contact regions are kept fixed.
• At the end of the second iterative procedure, a new contact analysis is performed to account for changes in the stiffness in the contact region.

This dual iteration process is repeated until convergence in both the contact and plasticity conditions is realized.

For an example of converting a linear elastic multi-body contact model to an elastic-plastic multi-body contact model, refer to Helpful Hints and Tips: Converting Linear-Elastic Contact to Elastic-Plastic Contact.

Multi-Body Contact Post-Processing

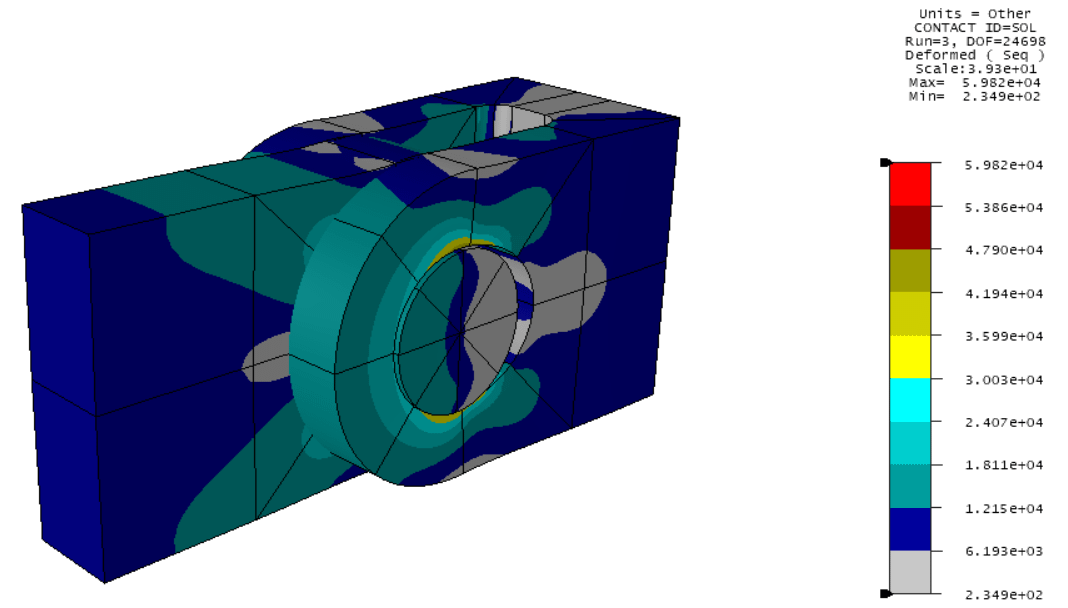
Once the multi-body analysis is complete, the user may post-process as with any linear analysis and perform the Key Quality Checks for FEA Solution Verification:

• Check that the “Max Contact Pressure Error” is reasonable for the model inputs (assuming no knife edge effects are present).
• Plot the deformed shape using both autoscale and 1:1 scaling. It may be helpful to use the Cutting Plane to visualize deformations in obscured regions.
• Plot fringe contours of the function of interest (e.g. S1) to ensure there are no significant jumps across element boundaries.
• If a p-extension was performed, verify that the maximum data of interest converged within a reasonable error.

Contact Pressure and Gap Functions

In addition, the following functions are available for post-processing of multi-body contact analysis results:

• Contact Press.: the contact pressure
• Initial Gap: the initial measured gap before the multi-body contact iterations
• Final Gap: the final measured gap after the multi-body contact iterations are completed. Too much penetration detected?

It is recommended to plot/extract these functions for each body in contact to ensure the behavior is as expected. Below is an animation of plotting the Final Gap function:

For more information on plotting the contact pressure, initial gap and final gap, refer to StressCheck Tutorial: Multi-Body Contact Solver Options/Plot Functions.

Computing Load Transfer

Additionally, the stress resultant (Resultant tab) for element faces in contact (Select > Face/Face Surface > Selection) or contact zones (Select > Contact Zone > Selection) should be extracted to verify load transfer between contact zones. Below is an animation of checking the resultant for a Face Surface selection:

See “Resultants and Multi-Body Contact” in the following FAQ for more information on extracting the resultant: How Can I Check Load Transfer, Equilibrium and Nodal Reactions In Results?

Influence of Stress Singularities on Resultants

Stress singularities due to knife edge effects (i.e. sharp corners of one body penetrating another body) can lead to differences in resultant computation. In this case, it may be required to select additional elements outside the contact zones to capture the “pressure bleed” resulting from the knife edge effect.

For an example of incorporating additional element faces outside the contact zones to improve the resultant computation, refer to StressCheck Tutorial: Influence of Stress Singularities On Multi-Body Contact Resultant Calculations.

A Note On Error Estimation

When performing a sequence of linear solutions with contact, the estimated relative error in energy norm may not be reliable. This is because the contact condition and the load vector are not the same for each p-level. Consequently, a slightly different problem is solved for each p-level which affects the error estimator. However, the sequence of solutions should be used to ascertain the convergence of the data of interest.

For more information on common multi-body contact issues, refer to What Are Some Common Multi-Body Contact Issues?

Was this article helpful?

0 out Of 5 Stars

5 Stars		0%
4 Stars		0%
3 Stars		0%
2 Stars		0%
1 Stars		0%

5 Submit

How can we improve this article?

Please submit the reason for your vote so that we can improve the article.

Submit